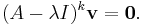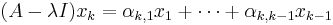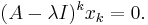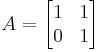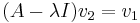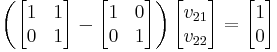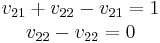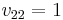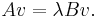Generalized eigenvector

In linear algebra, for a matrix A, there may not always exist a full set of linearly independent eigenvectors that form a complete basis – a matrix may not be diagonalizable. This happens when the algebraic multiplicity of at least one eigenvalue λ is greater than its geometric multiplicity (the nullity of the matrix 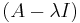$(A-\lambda I)$ , or the dimension of its nullspace). In such cases, a generalized eigenvector of A is a nonzero vector v, which is associated with λ having algebraic multiplicity k ≥1, satisfying

$(A-\lambda I)^k\mathbf{v} = \mathbf{0}.$

The set of all generalized eigenvectors for a given λ form the generalized eigenspace for λ.

Ordinary eigenvectors and eigenspaces are obtained for k=1.

1 For defective matrices
2 Example
3 Other meanings of the term
4 See also
5 References

For defective matrices

Generalized eigenvectors are needed to form a complete basis of a defective matrix, which is a matrix in which there are fewer linearly independent eigenvectors than eigenvalues (counting multiplicity). Over an algebraically closed field, the generalized eigenvectors do allow choosing a complete basis, as follows from the Jordan form of a matrix.

In particular, suppose that an eigenvalue λ of a matrix A has an algebraic multiplicity m but fewer corresponding eigenvectors. We form a sequence of m eigenvectors and generalized eigenvectors 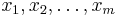$x_1, x_2, \ldots, x_m$ that are linearly independent and satisfy

$(A - \lambda I) x_k = \alpha_{k,1}x_1%2B\cdots%2B\alpha_{k,k-1}x_{k-1}$

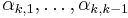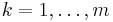for some coefficients $\alpha_{k,1},\ldots,\alpha_{k,k-1}$ , for $k=1,\ldots,m$ . It follows that

$(A - \lambda I)^k x_k = 0. \!$

The vectors 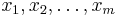$x_1, x_2, \ldots, x_m$ can always be chosen, but are not uniquely determined by the above relations. If the geometric multiplicity (dimension of the eigenspace) of λ is p, one can choose the first p vectors to be eigenvectors, but the remaining m − p vectors are only generalized eigenvectors.

Example

$A = \begin{bmatrix} 1 & 1\\ 0 & 1 \end{bmatrix}$

Then there is one eigenvalue λ=1 with an algebraic multiplicity m of 2.

There are several ways to see that there will be one generalized eigenvector necessary. Easiest is to notice that this matrix is in Jordan normal form, but is not diagonal, meaning that this is not a diagonalizable matrix. Since there is 1 superdiagonal entry, there will be one generalized eigenvector (or you could note that the vector space is of dimension 2, so there can be only one generalized eigenvector). Alternatively, you could compute the dimension of the nullspace of 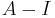$A-I$ to be p=1, and thus there are m-p=1 generalized eigenvectors.

Computing the ordinary eigenvector 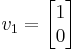$v_1=\begin{bmatrix}1 \\0 \end{bmatrix}$ is left to the reader (see the eigenvector page for examples). Using this eigenvector, we compute the generalized eigenvector 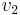$v_2$ by solving

$(A-\lambda I)v_2 = v_1$

Writing out the values:

$\left(\begin{bmatrix} 1 & 1\\ 0 & 1 \end{bmatrix}- \begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix}\right)\begin{bmatrix}v_{21} \\v_{22} \end{bmatrix} = \begin{bmatrix}1 \\0 \end{bmatrix}$

This simplifies to

$\begin{matrix} v_{21}%2Bv_{22}-v_{21} = 1 \\ v_{22}- v_{22} = 0 \end{matrix}$

This simplifies to

$v_{22}= 1$

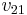And $v_{21}$ has no restrictions and thus can be any scalar. So the generalized eigenvector is 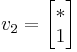$v_2=\begin{bmatrix}* \\1 \end{bmatrix}$ , where the * indicates any value is fine. Usually picking 0 is easiest.

Other meanings of the term

The usage of generalized eigenfunction differs from this; it is part of the theory of rigged Hilbert spaces, so that for a linear operator on a function space this may be something different.

One can also use the term generalized eigenvector for an eigenvector of the generalized eigenvalue problem

$Av = \lambda B v.$

References

Axler, Sheldon (1997). Linear Algebra Done Right (2nd ed.). Springer. ISBN 978-0387982588.

Generalized eigenvector

Contents

For defective matrices

Example

Other meanings of the term

See also

References